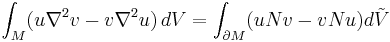Green's identities
In mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.
Contents |
Green's first identity
This identity is derived from the divergence theorem applied to the vector field 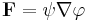 : Let φ and ψ be scalar functions defined on some region U in R3, and suppose that φ is twice continuously differentiable, and ψ is once continuously differentiable. Then[1]
: Let φ and ψ be scalar functions defined on some region U in R3, and suppose that φ is twice continuously differentiable, and ψ is once continuously differentiable. Then[1]
where 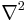 is the Laplace operator,
is the Laplace operator,  is the boundary of region U and n is the outward pointing unit normal of surface element dS. This theorem is essentially the higher dimensional equivalent of integration by parts with ψ and the gradient of φ replacing u and v.
is the boundary of region U and n is the outward pointing unit normal of surface element dS. This theorem is essentially the higher dimensional equivalent of integration by parts with ψ and the gradient of φ replacing u and v.
Note that Green's first identity above is a special case of the more general identity derived from the divergence theorem by substituting  :
:
Green's second identity
If φ and ψ are both twice continuously differentiable on U in R3, and ε is once continuously differentiable:
For the special case of 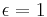 all across U in R3 then:
all across U in R3 then:
In the equation above ∂φ / ∂n is the directional derivative of φ in the direction of the outward pointing normal n to the surface element dS:
Green's third identity
Green's third identity derives from the second identity by choosing  , where G is a fundamental solution of the Laplace equation. This means that:
, where G is a fundamental solution of the Laplace equation. This means that:
For example in 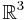 , the fundamental solution has the form:
, the fundamental solution has the form:
Green's third identity states that if ψ is a function that is twice continuously differentiable on U, then
A further simplification arises if ψ is itself a harmonic function, i.e. a solution to the Laplace equation. Then  and the identity simplifies to:
and the identity simplifies to:
On manifolds
Green's identities hold on a Riemannian manifold, In this setting, the first two are
where u and v are smooth real-valued functions on M, dV is the volume form compatible with the metric,  is the induced volume form on the boundary of M, N is oriented unit vector field normal to the boundary, and
is the induced volume form on the boundary of M, N is oriented unit vector field normal to the boundary, and 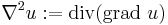 is the Laplacian.
is the Laplacian.
See also
External links
- [1] Green's Identities at Wolfram MathWorld
Reference
- ^ Strauss, Walter. Partial Differential Equations: An Introduction. Wiley.


![\int_U \left[ \psi \nabla \cdot \left( \epsilon \nabla \varphi \right) - \varphi \nabla \cdot \left( \epsilon \nabla \psi \right) \right]\, dV = \oint_{\partial U} \epsilon \left( \psi {\partial \varphi \over \partial n} - \varphi {\partial \psi \over \partial n}\right)\, dS.](/2012-wikipedia_en_all_nopic_01_2012/I/a76546f5aca45a041bdd386401217d98.png)

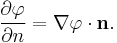
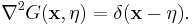

![\int_U \left[ G(\mathbf{y},\mathbf{\eta}) \nabla^2 \psi(\mathbf{y})\right]\, dV_\mathbf{y} - \psi(\mathbf{\eta})= \oint_{\partial U} \left[ G(\mathbf{y},\mathbf{\eta}) {\partial \psi \over \partial n} (\mathbf{y}) - \psi(\mathbf{y}) {\partial G(\mathbf{y},\mathbf{\eta}) \over \partial n} \right]\, dS_\mathbf{y}.](/2012-wikipedia_en_all_nopic_01_2012/I/fef563f84d3c2c6c9fbf61ce64f0878d.png)
![\psi(\mathbf{\eta})= \oint_{\partial U} \left[\psi(\mathbf{y}) {\partial G(\mathbf{y},\mathbf{\eta}) \over \partial n} - G(\mathbf{y},\mathbf{\eta}) {\partial \psi \over \partial n} (\mathbf{y}) \right]\, dS_\mathbf{y}.](/2012-wikipedia_en_all_nopic_01_2012/I/c84ce3a7c22b016651c2344cf55c2159.png)